Acoustique

Construire son studio

Evitez les problèmes majeurs !

Plutôt que de multiplier les corrections, il vaut mieux éviter les erreurs.
Assurez vous d'abord que les lieux conviennent à l'utilisation à laquelle vous des destinez. Il serait dommage d'investir dans le traitement acoustique d'un local qui s'avérerait inutilisable une fois terminé.

Il faut d'abord distinguer l'isolation phonique du traitement acoustique. Une bonne isolation phonique garantit l'indépendance à l'égard des nuisances venues de l'extérieur ou que vous pourriez émettre.
L'isolation phonique est un domaine trop vaste pour être convenablement traité en détails dans ce chapitre et notre propos se limitera essentiellement à la correction acoustique.

Cependant, vos portes et fenêtres sont-elles suffisamment étanches ?

Existe-t-il un conduit de cheminée ?

Les conduites d'eau et de chauffage sont-elles communes aux autres étages ?

Le local est-il situé près d'un carrefour ou d'une ligne de métro ?

Posez-vous ces questions et examinez chaque détail. En cas de doute, consultez un acousticien. Vous réaliserez des économies substantielles.

Les ondes sonores
Pour mieux appréhender les phénomènes auxquels vous serez confronté, il est bon de rappeler quelques lois élémentaires.

Lorsque l'on joue d'un instrument de musique dans une pièce, le son se propage dans toutes les directions en ondes sphériques concentriques. Une partie de cette énergie parvient en ligne droite à nos oreilles. Il s'agit du champ direct.

Le reste va rencontrer les parois du local (murs, sols, plafonds). En l'absence de traitement, ces parois réfléchissent la plus grande partie de l'énergie dans des centaines de directions. Les réflexions reviennent à nos oreilles avec un décalage temporel car le chemin parcouru est plus long. On parle alors de champ réfléchi ou de champ réverbéré.

	Le champ réfléchi : ami ou ennemi ?
	Pour le savoir il faut distinguer les premières réflexions, l'écho et la réverbération. En fait, seule la réverbération bien maîtrisée nous intéresse, les autres réflexions restent des phénomènes indésirables.

	Premières réflexions
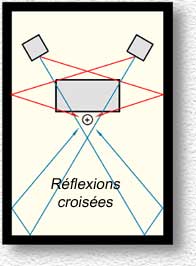
	Prenons le cas d'une régie ou d'un auditorium. Comme nous venons de le voir, le son émis par les enceintes n'est pas dirigé seulement vers le point d'écoute. Les ondes sonores rayonnent dans toutes les directions. Si les murs sont nus ou peu absorbants, elles vont s'y réfléchir parcourant un chemin détourné avant de parvenir aux oreilles de l'auditeur.

Effet de fusion

Notre cerveau met du temps pour intégrer certains événements. Lorsque nous regardons un film par exemple, l'animation ne devient fluide qu'à la cadence minimale de 16 images par seconde. De même, en deçà de 50 millisecondes environ nous ne savons pas séparer les réflexions du signal source. Les deux nous parviennent dans ce que nous pourrions appeler une sorte de fusion. Tant que l'écoute est monophonique, l'effet est plutôt agréable car il tend à augmenter le niveau sonore global.


Mais dès qu l'on se trouve confronté à plusieurs sources on perd les points de repères. Le cumul du son direct et des premières réflexions produit un signal brouillé et confus qui ne permet pas une spatialisation correcte de l'image sonore ni une bonne séparation des canaux.

Les réflexions dont le retard est supérieur à 50 ou 80 millisecondes (la transition est progressive), sont mieux perçues. La séparation entre champ direct et champ réverbéré est plus distincte et la notion de volume de la pièce devient plus évidente.

Echo et réverbération

Dans une pièce vide, frappez dans vos mains. Les centaines de réflexions sur les parois et obstacles de la pièce produisent une traînée sonore dont l'amplitude décroît rapidement. Si les réflexions sont uniformément réparties sur la durée de la traînée et que la décroissance est régulière, il s'agit d'une réverbération.

Si par contre, on entend distinctement une répétition du claquement de mains, il s'agit d'un écho flottant (flutter echo), c'est-à-dire que deux surfaces parallèles se renvoient le signal. Pour mieux appréhender les phénomènes auxquels vous serez confronté, il est bon de rappeler quelques lois élémentaires.

Ondes stationnaires et échos flottants

Les ondes se réfléchissent aussi dans le mode axial, tangentiel et oblique de la pièce. C'est ce qu'on appelle les modes propres. Le plus dangereux étant le mode axial que l'on retrouve dans le sens longitudinal, transversal et vertical de la pièce. Si les proportions de celle-ci n'entrent pas dans un rapport optimal, les résonances engendrées à certaines fréquences vont se cumuler créant ainsi des pics d'ondes stationnaires qui se manifestent par la présence d'échos flottants.

Des murs non parallèles vont atténuer ce phénomène et sans certitude de le supprimer. L'idée qu'une pièce aux murs non parallèles sonne forcément bien n'est qu'une superstition.

	Proportions optimales
	Pour éviter le cumul des résonances coïncidentes qui conduisent toujours à des colorations et des échos désagréables, il est souhaitable que le rapport des dimensions du local vide favorise une distribution homogène des réflexions. Même si vous n'avez pas le choix, la pièce étant déjà construite, il est utile d'avoir des points de repère pour comprendre l'origine de certains phénomènes.

	L'important est d'obtenir un espacement et une amplitude des réflexions aussi réguliers que possible. Plusieurs acousticiens célèbres ont trouvé des rapports de proportions favorables. Parmi eux, Bolt propose un diagramme intéressant : Lorsque la longueur et la largeur divisées par la hauteur entrent dans le diagramme ci-contre, les proportions sont acceptables. A condition bien sûr d'éviter les multiples francs 1,5 - 2 - 2,5 - 3 etc... qui favorisent le cumul des harmoniques.

D'après Sepmeyer le rapport 1: 1,6 : 2,33 est excellent (soit 4mx5,83m pour une hauteur de 2,5m).
Si vous ne pouvez pas ramenez les proportions de la pièce à ces valeurs, ne paniquez pas rien n'est perdu. Il faudra seulement surveiller les fréquences critiques et envisager un traitement adéquat. Evitez quand même les surfaces carrées. Si votre pièce est un cube parfait, fuyez !


Concentration de l'énergie dans les angles
Toute pièce ayant au moins deux parois parallèles résonne aux fréquences liées aux longueurs d'onde de la pièce. La pression acoustique est maximum sur les parois, elle double ou triple dans les angles. C'est donc là que l'on va trouver les pressions acoustiques réfléchies les plus élevées aux fréquences basses. Pour vous en convaincre, diffusez un programme musical et placez-vous dans un angle de la pièce les oreilles près du mur. La résonance audible vous renseigne sur la concentration de l'énergie sonore en cet endroit. Ce phénomène est la source de colorations indésirables.

Filtrage en peigne

Les réflexions axiales, tangentielles et obliques engendrées par les modes propres créent des nœuds de pression. Si vous avez la possibilité de diffuser un bruit rose ou à défaut, un programme riche en fréquences élevées (cymbales, applaudissements), marchez lentement dans la pièce. Par endroits, vous entendrez un effet de phasing. Les réflexions à décalage fixe produisent un filtrage en peigne très symptomatique. Ce phénomène est hélas, largement répandu dans de nombreux studios.

Les solutions

Pour traiter convenablement une pièce, on dispose de quatre principes acoustiques fondamentaux : l'absorption, la réflexion, la diffraction et la diffusion.

Absorption/réflexion

Lorsqu'une onde sonore rencontre un matériau, une partie de l'énergie incidente est absorbée, le reste est réfléchi. L'absorption se mesure en Sabines. Chaque matériau possède un coefficient qui correspond à un pourcentage d'absorption. Ce coefficient varie avec la fréquence et l'angle d'incidence.
Il s'exprime en alpha Sabines. Par exemple, un coefficient de 0.55

S signifie que 55% de l'énergie sonore est absorbée et par conséquent 45% réfléchie. Un coefficient de 1

S correspond à une absorption infinie. Celle que l'on peut observer dans un espace sans obstacle (depuis une montgolfière par exemple).

Absorption

Note: certains matériaux absorbants affichent des coefficients supérieurs à 1. Cela vient de la méthode de mesure qui est effectuée en chambre réverbérante. L'énergie sonore atteint le matériau sous différents angles d'incidence et un facteur de correction est appliqué. Cette méthode est la plus proche d'une situation réelle, mais les interprétations sont multiples. La mesure par la méthode du tube de Kundt, plus reproductible, ne prend en compte que les ondes qui de déplacent dans le sens perpendiculaire au matériau. Soyez vigilant, il y va des coefficients d'absorption comme des watts pour les amplis, on trouve de tout et n'importe quoi.

Réflexion

La diffraction

Toute surface réfléchissante dévie la trajectoire d'une onde sonore un peu comme un miroir dévie un rayon lumineux. Ceci est vrai à condition que la taille de l'obstacle soit supérieure à la longueur d'onde du signal. Les zigzags, les surfaces convexes et les reliefs accidentés (improprement appelés diffuseurs) sont intéressants pour casser les échos flottants et liés à la présence d'ondes stationnaires. Les surfaces de réflexion planes sont utiles pour modifier les proportions apparentes de la pièce. Les surfaces concaves sont à éviter car elles focalisent l'énergie en un point, et créent des nœuds de pression dont les conséquences sont catastrophiques.

Diffraction

La diffusion

Imaginez un rayon lumineux qui heurte la surface d'un miroir. L'image réfléchie sera nette et son contour bien délimité. Remplaçons maintenant le miroir par un mur blanc et mat.L'image réfléchie sera diffuse, sans contour précis. Pour obtenir la diffusion d'une onde sonore, le processus s'inspire du même principe mais il est un peu plus complexe.

Il ne suffit pas que l'onde rencontre un relief géométrique plus ou moins accidenté. Pour qu'il y ait une diffusion homogène et uniformément répartie, la géométrie de l'obstacle doit répondre à des lois physiques précises. Deux formules mathématiques parmi quelques unes répondent aux critères de diffusion et donne des résultats satisfaisants sous différents angles d'incidence. Il s'agit de l'application intelligente du principe du gradient de phase avec la séquence à résidu quadratique issu des travaux de Schroeder et la séquence à racine primitive. Méfiez-vous des recettes miracle et de s machins en matières synthétique vendus sous le nom de diffuseurs et qui ne sont en fait que des diffracteurs. Au mieux, ils atténueront les effets des ondes stationnaires mais ils ne pourront pas créer le champ diffus sous différents angles d'incidence, essentiel à l'obtention d'une réverbération homogène.